
 繁体
繁体
第一百五十七章 朕就是这样的人,小肚鸡肠(2/4)
数轴可以表示任何一个整数和任何一个循环小数,因为循环小数可以转化成任何两个整数的比。
数字的图形意义就是 。
。
“以一厘为长度,开始将这条直线切割 来,便有了,…-3、-2、-1、0、1、2、3…如果我们需要更
来,便有了,…-3、-2、-1、0、1、2、3…如果我们需要更 准,就把一厘分成十毫,如此重重。”
准,就把一厘分成十毫,如此重重。”
题板之上,画着一个个的小方格,还有纵横的两条轴,而在题板之上,有一个近乎于完 的曲线,这个曲线,张居正一
的曲线,这个曲线,张居正一 就看了
就看了 来,就是之前皇帝陛下研究如何制作看的更清楚、没有
来,就是之前皇帝陛下研究如何制作看的更清楚、没有 差、更加稳定的反
差、更加稳定的反 千里镜所画的曲线。
千里镜所画的曲线。
“皇叔的十二平均律,已经证实了,√2、√3它是一个无限的不循环的小数,不能表示为两个整数的比。”
“所以在一条直线我们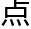 一个
一个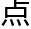 ,规定为零,就有了起
,规定为零,就有了起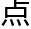 。”
。”
“先生,朕的算学略有
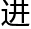 ,先生随朕来。”朱翊钧站了起来,来到了文华殿的偏殿。
,先生随朕来。”朱翊钧站了起来,来到了文华殿的偏殿。
“似乎我们可以利用这条数轴表示我们已知的所有的数,整数、分数、小数。”朱翊钧看着这 数轴说
数轴说 :“但是朕又遇到了一个新的麻烦,比如一个面积为4的正方形,边长为二,可以在带有刻度的数轴上表示
:“但是朕又遇到了一个新的麻烦,比如一个面积为4的正方形,边长为二,可以在带有刻度的数轴上表示 来,但如果是面积为3的正方形,边长是√3,这个数字在数轴上如何去表示呢?”
来,但如果是面积为3的正方形,边长是√3,这个数字在数轴上如何去表示呢?”
小皇帝看张居正带了几万层的滤镜,那自然觉得张居正的学问也是极好的,但是张居正自问学问,还是不如王 明的,他就是个当官的。
明的,他就是个当官的。
“而在王文素的《算学宝鉴》之中,有数形结合之思想,数字和形状,存在一 普遍的联系,有形则有数,有数亦有形,就像矛盾,从来不是孤立存在的。”
普遍的联系,有形则有数,有数亦有形,就像矛盾,从来不是孤立存在的。”
大明的度量衡尤其是度数 下还是百分制,而不是六十分制度,圭表之上一刻等于一百分,一分等于一百秒,这是大明在天文学上的数形结合。
下还是百分制,而不是六十分制度,圭表之上一刻等于一百分,一分等于一百秒,这是大明在天文学上的数形结合。
“朕之前制作反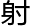 千里镜,研究千里镜制作的时候,就在思索,反
千里镜,研究千里镜制作的时候,就在思索,反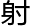 千里镜的倍数,又该如何确定?”
千里镜的倍数,又该如何确定?”
“一个数,在图形上也有它的意义,比如0,通常表示没有,那么在很多时候,也表示开始,从零开始,那么数字便有了形的意义。”
朱翊钧用尺 画了一
画了一 直线,笑着说
直线,笑着说 :“《易》曰:上古结绳而治,后世圣人易之以书契。事大,大结其绳;事小,小结其绳,结之多少,随
:“《易》曰:上古结绳而治,后世圣人易之以书契。事大,大结其绳;事小,小结其绳,结之多少,随 众寡。”
众寡。”
愚 的蠢事,张居正知
的蠢事,张居正知 后,也直接认了错,不对就是不对。
后,也直接认了错,不对就是不对。
“臣遵旨。”张居正想了想,也是这个 理,他的学问虽然不
理,他的学问虽然不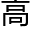 ,但是讲的内容都是切切实实的
,但是讲的内容都是切切实实的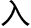 世治理的学问,大明科举要的是官员,而不是经学博士。
世治理的学问,大明科举要的是官员,而不是经学博士。
“先生,朕以为,天下四书的注解,还是得以先生注解为准,那余懋学说王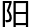 明要从祭孔庙,但是王门七派,基本都没有了行,也就没有了实,还是先生的注解比较好。”
明要从祭孔庙,但是王门七派,基本都没有了行,也就没有了实,还是先生的注解比较好。”
张居正无奈的说 :“新建伯的才学比臣要
:“新建伯的才学比臣要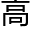 ,臣为陛下讲筵,陛下自然以为臣的才学
,臣为陛下讲筵,陛下自然以为臣的才学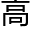 。”
。”
张居正当然能够理解这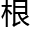 普通的线有了
普通的线有了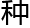
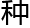 定义之后,就可以成为一
定义之后,就可以成为一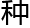 数学工
数学工 ,因为这
,因为这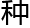 数学工
数学工 在度数旁通之中,使用的非常频繁。
在度数旁通之中,使用的非常频繁。
说到这里,朱翊钧停了下来,祖冲之从来不认为圆周率可以被表示为两个整数的比,他 确的计算
确的计算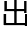 了圆周率位于朒数和盈数之间。
了圆周率位于朒数和盈数之间。
同样为了方便计算,祖冲之也给了两个近似值一个名字叫约率为22/7,一个叫密率为355/113,直到万历年间为法兰西效力的韦达,才计算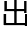 了355/113这一数值。
了355/113这一数值。
厚重的帷幕拉开,正午不太 烈的
烈的 光,照在了那块题板之上。
光,照在了那块题板之上。
朱翊钧颇有
 的说
的说 :“很好,先生大才。”
:“很好,先生大才。”
朱翊钧则摇 说
说 :“标准不同罢了,先生的是
:“标准不同罢了,先生的是 世治国的学问,朕看过了
世治国的学问,朕看过了 明心学,不敢说七派都明白,但是王门弟
明心学,不敢说七派都明白,但是王门弟 ,多数都走
,多数都走 了岔路里,借着新建伯的名
了岔路里,借着新建伯的名 ,招摇撞骗者众。”
,招摇撞骗者众。”
“先生怕他们学不明白?朕都能学的明白,他们应该可以的。”朱翊钧笑着说 。
。
朱翊钧站在题板之前,颇为郑重的说 :“先生之前讲矛盾说,说月随地动月照影生,树随风动树摆叶随,
:“先生之前讲矛盾说,说月随地动月照影生,树随风动树摆叶随, 随叶动湖生涟漪,天下万
随叶动湖生涟漪,天下万 无不存在普遍联系。”
无不存在普遍联系。”
“正算赤,负算黑,所以这条直线就有了方向,向右为正,向左为负。”
朱翊钧画 了一条数轴来,大明的数轴运用的极为普遍,比如天球,比如天赤
了一条数轴来,大明的数轴运用的极为普遍,比如天球,比如天赤 ,比如黄赤
,比如黄赤 角、比如岁差计算、比如圭表影长、比如北天地极
角、比如岁差计算、比如圭表影长、比如北天地极 地角度等等,这都是数轴或者说数形结合的
地角度等等,这都是数轴或者说数形结合的
 应用。
应用。
“先生,天下学政败坏如此,若是先生还不肯教化,那 下朕有先生辅弼,先生之后呢?朕又用何人?朕之后呢?我大明再用何人?就这么定了。”
下朕有先生辅弼,先生之后呢?朕又用何人?朕之后呢?我大明再用何人?就这么定了。”
张居正其实对自己的教学能力并没什么信心,他的弟 ,小皇帝,在刺王杀驾之前,也是厌学;傅应祯直接
,小皇帝,在刺王杀驾之前,也是厌学;傅应祯直接 脆当殿弹劾张居正他这个座主;
脆当殿弹劾张居正他这个座主; 启愚搞
启愚搞 了应天府乡试以《舜亦以命禹》为提;再看李乐,吃人家的拿人家的还不办事。
了应天府乡试以《舜亦以命禹》为提;再看李乐,吃人家的拿人家的还不办事。
朱翊钧拿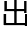 了一个圭表,笑着说
了一个圭表,笑着说 :“刻分秒。”
:“刻分秒。”
但是一个无限不循环的小数,又
