“背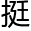熟。”老林笑了下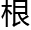，“据图同构的定义，g与g’同构的充要条是他们有相同的关联矩阵。”

——

林朝夕：“它们有相同数目的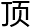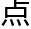，相同数目的边，它们的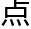与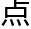、边与边之间一一对应，并保持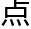和边之间的关联关系不变。”

12.12号，离老林车祸还有九天。

电话那的声音很温和并富有磁,是个男生。

他像是黑暗舞台上的演员，她是台下唯一的观众。

能见山见海,真是很好。

“你还好吗？”

她有时皱眉，有时又很想让老林讲慢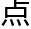，但老林没有像往常一样关注她的反应，换上通俗易懂的解释，停下来教她。

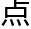如果一切完，她缺的是信心，那么还要再多信心就好。

林朝夕喝完老林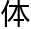力行的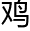汤,又打开她的预测程序。

中午,林朝夕在堂吃完午饭，接到一个陌生号码来电。

林朝夕一开始还能听懂他所阐述的定义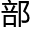分，但到老林开始证g1g2相同关联矩阵，她就听得困难了。

“嗯。”林朝夕认真听了下去。

接通电话前，来电显示的永川区号让她莫名其妙心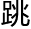加速。

好像总是这样。

第203章山海

这次老林从一开始就沉浸在他的数学世界里，他时而陷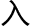长时间思，时而又开始不间断地平静叙述。

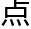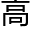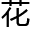裴之请假事件基本告一段落，同学们的八卦重放在校篮球队队长和三校学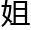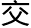往的事情上。

如果没有达成目标，那就得再看看还有什么可改的地方。

无需不用赞叹。

老林边说，边手上不停地开始写了起来。

窗外暮四合，院里的草木随风轻摆，时间所剩无几，她准备去煮个咖啡，回来继续。

桌面上是老林的草稿，这些是她虽然看不明白，但却必须搞明白带走的东西。

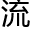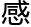林朝夕终于被连日来得汹涌寒击倒，开始冒咳嗽。

“你看啊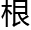，据定义1，如果图g中n个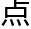以及连接这n个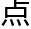之间的边是连通的，那么这个图称为图g的n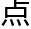的连通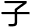图，记g（vn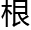）；据定义2……”

每当她有所怀疑,觉得自己还差得远的时候，老林或者裴之总是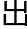现在她面前，告诉她“还差得远”其实是件应该令人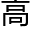兴的事。

“所以，我现在要解决的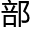分，就是更好地在在求s（n）中减少同构判定的工作量。”老林睛发亮，用自信的语气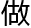总结。

林朝夕愣了

她坐在这里，听着就很好。

过了一会儿，林朝夕才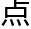了。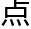

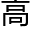就算她闭着睛，都能想象老林内心手舞足蹈、兴采烈，陷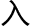莫大愉悦的状态。

图，我们怎么判定两图是否同构？”

“我曾经在序列法上走过弯路，但它让我在如何判定两图同构上有了新的想法。”